Lab Report
Individual Report
Due date: Friday, 10 November, 2023, 23:59
Include: Code, figures, and anything you think it is important :)
Question 1 (25 Pts.)
Given the following dynamic system ${m}\ddot{x}+4\dot{x}+8x=3u$, for $m=2$ and $u$ as the input, with initial conditions
$x(0)=0$ and $\dot x(0)=0$. Manually calculate the transfer function and represent
it in Matlab/Ocatve. Calculate the Laplace transformation's partial fraction decomposition (i.e. [r, p, k])
by Matlab/Octave and write down the complete form (i.e. the function) in your lab report.
Question 2 (25 Pts.)
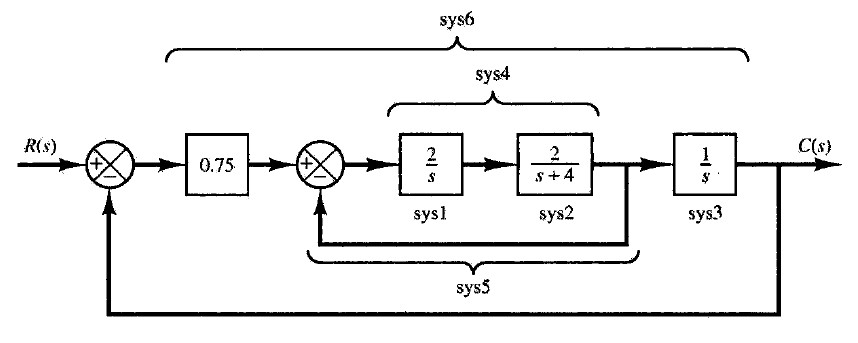
Compute the total transfer function $C/R$ of the following system, compute the poles, draw the pole-zero map and the root locus
using Matlab/Octave.
Question 3 (25 Pts.)
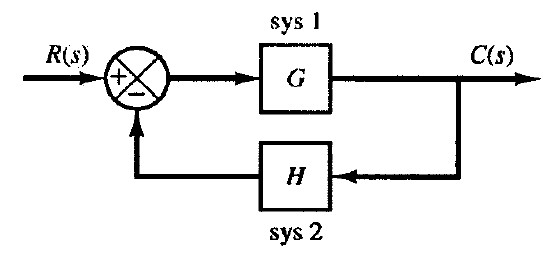
Consider the following negative feedback system,
where
$$G(s)=\frac{5(s + 20)}{s(s + 4.5883)(s^2 + 3.4118s + 16.346)}$$
and $H=6$. Using matlab/octave, calculate the transfer function $C/R$, the unit step response, the impulse response, and the time response
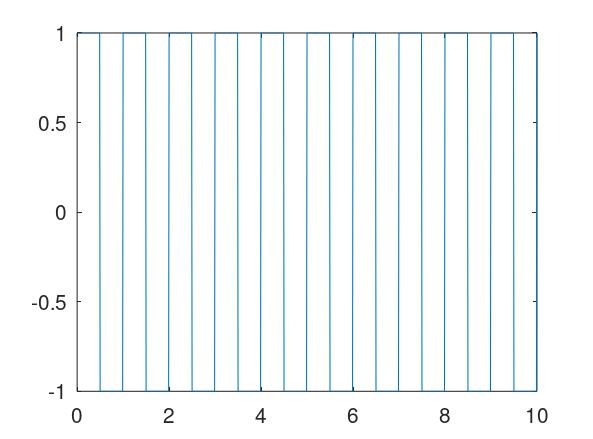
with a square wave input of period 5s with amplitude 1 of the closed-loop system.
Hint: the syntax of generating square wave in Matlab is
For example, to generate a square wave of period 1s with amplitude 1, we can use the following scripts.
t = 0:0.001:10;
f = square(2*pi*t);
plot(t,f);
Note that if you are using Octave, you need to add "pkg load signal;" at the beginning of the script.
Run the scripts, we can get the figure of the square wave;
Question 4 (25 Pts.)
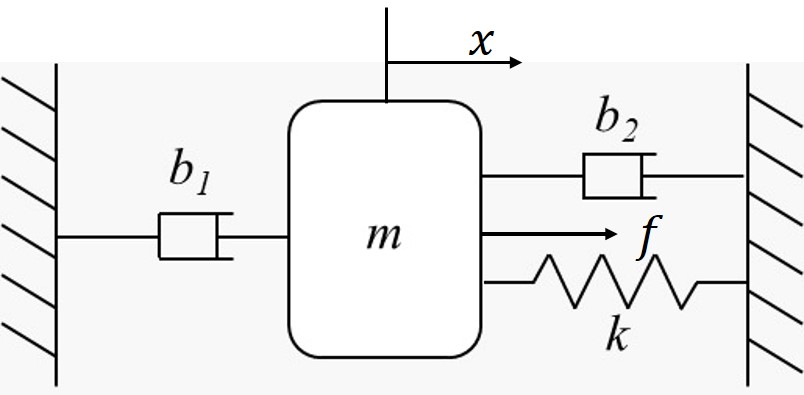
Consider the following mass-damper-spring system,
Suppose we have $m=1$, $b_1=2$, $b_2=3$, $k=1$, $\dot x(0)=0$ and $x(0)=0$, use the ODE solver to create
a simulation to show the response of $x$ under a constant force $f=1.5$.
Hint: For a second-order system $\ddot{x}+b\dot{x}+cx=u$, denote
$x_1=x, x_2=\dot{x}$, then the system can be rewritten as
$$\left\{\begin{aligned}
& \dot x_1=x_2\\
& \dot x_2 = -bx_2-cx_1+u
\end{aligned}\right.$$